
Class 12th maths notes chapter 1 Relationship and function ex1.3
इस लेख में, हमने MP board class 12th maths book solution chapter 1 relation and function pdf साझा की हैं, ये हल 12वीं गणित के छात्रों के लिए अति महत्वपूर्ण है। ये समाधान नवीनतम एमपी बोर्ड पुस्तकों के विषय विशेषज्ञों द्वारा हल किए गए हैं।
MP Board Class 12th Maths Solutions Chapter 1 संबंध एवं फलन Ex 1.3
मान लीजिए कि f:{1, 3, 4} → {1, 2, 5} तथा g:{1, 2, 5} → {1, 3}, f = {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त है। gof ज्ञात कीजिए।
हल:दिया है:
f = {(1, 2), (3, 5)(4, 1)}
तथा g = {(1, 3),(2, 3), (5, 1)}
∴ gof(1) = g (f (1))
= g(2)
= 3
gof(3) = g(f (3))
= g(5)
= 1
तथा g of(4) = g(f(4))
= g(1)
= 3
∴ gof = {(1, 3), (3, 1), (4, 3)}
प्रश्न 2.
मान लीजिए कि f,g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g)oh = foh + goh
(f.g)oh = (foh).(goh)
हल:दिया है:
f: R → R, g: R → R, h: R → R
∴ (fog)oh(x) = (g + g)(h (x))
= g(h (x)) + g (h (x))
= (foh) (x) + (goh) (x)
= (foh + goh) (x)
∴ f(f + g) oh = foh + goh
पुनः (f.g) oh(x) = (f.g)(h (x))
= f (h (x)).g(h (x))
= (foh)x (goh) (x)
= [(goh) (goh)](x)
∴ (f.g)oh = (foh) (goh)
प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि
(i) f(x) = |x| तथा g(x) = |5x – 2|
(ii) f(x) = 8x³ तथा g(x) = x¹∕³
हल:(i) ∵ f(x) = |x|
तथा g(x) = [5x – 2||
∴ gof(x) = g[f (x)]
= g[/x]
= |5 |x – 2|
तथा fog (x) = f|g(x)|
= f (|5x – 2|)
= |5x – 2|
= |5x – 2|
(ii) ∵ f(x) = 8x³
तथा g(x) = x¹/³
∴ gof(x) = g[f (x)]
= g(8x³)
= (8x³)¹/³
= 2x
तथा fog(x) = f[g(x)]
= f(x¹/³)
= 8(x¹/³)³
= 8x
प्रश्न 4.
यदि f(x) = (4x+3)6x–4 , x ≠ 23 , तो सिद्ध कीजिए कि सभी x ≠ 23 के लिए f0f(x) = x है। का प्रतिलोम फलन क्या है?
हल:दिया है :

⇒ y (6x – 4) = 4x + 3
⇒ 6xy – 4y = 4x + 3
⇒ 6xy – 4x = 4y + 3
⇒ 6xy – 4x = 4y + 3
⇒ x =
अतः f का प्रतिलोम f ही है।
प्रश्न 5.
कारण सहित बतलाइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैं-
(i) f:{1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4),(8, 2}}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल:(i) दिया है : f :{1, 2, 3, 4} → {10) जहाँ
f = {(1, 10),(2, 10), (3, 10),(4, 10)}
∵ f(1) = 10, f(2) = 10, f(3) = 10, f(4) = 10
⇒ f(1) = f(2) = f(3) = f(4)
∴ f एकैक नहीं है।
अतः दिए गये फलन का प्रतिलोम नहीं है।
(ii) g = {5, 6,7, 8} → 1, 2, 3, 4) जहाँ
g = {(5, 4), (6, 3),(7, 4), (8, 2)}
∴ g (5) = 4 तथा g (7) = 4
∵ (5) = g (7) = 4
∴ एकैक नहीं है।
अतः दिये गये फलन का प्रतिलोम नहीं है।
(iii) h : {2, 3, 4, 5} → {7, 11, 13} जहाँ
h = {(2, 7),(3, 9),(4, 11), (5, 13)}
∴ h (2) = 7, h (3) = 9, h (4) = 11 तथा h (5) = 13
∴ h एकैक है
अतः दिए गए फलन (h) का प्रतिलोम है।
प्रश्न 6.
सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = xx+2 , द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
हल:यदि f(x1) = f(x2) तब,
![सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = , द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए। सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = , द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhgjCOFNpAbBtSOyl18Bff-VVIc1nV7qVeFCaR_4lq1E8DkyqiK2Dy-1z5st2c9J5V7LCP4kR4EiEd7g1Al0em2PrFwpgDj0B-bCVjVMqqpRYpRsbiWVNY9L_ByF0nc4VKBTVklduYYqPc/s16000/IMG_20210108_123930.png) |
प्रश्न 7.
f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। का प्रतिलोम फलन ज्ञात कीजिए।
हल:फलन f : R → R निम्न द्वारा परिभाषित है
f(x) = 4x + 3
यदि f(x₁) = f(x₂)
⇒ 4x₁ + 3 = 4x₂ + 3
⇒ x₁ = x₂
∴ f एकैक है।
तथा माना f(x) = y = 4x + 3
⇒ 4x = y – 3
⇒ x =
सहप्रान्त (Co – domain) प्रत्येक अवयव yE R का प्रान्त (do main) में पूर्व प्रतिबिम्ब (pre image) है।
∴ f आच्छादक (onto) है
अतः f एकैक और आच्छादक है।
अत: f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f-1 (y) = g(y)
=
प्रश्न 8.
f(x) = x² + 4 द्वारा प्रदत्त फलन f : R → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f का प्रतिलोम f-¹, f-¹(y) = y−4−−−−√ , द्वारा प्राप्त होता है, जहाँ R सभी ऋणेत्तर वास्तविक संख्याओं का समुच्चय है।
हल:यदि f(x₁) = f(x₂)
⇒ x₁² + 4 = x₁² + 4
⇒ x₁² = x₂² = x₁ = x₂
( ∵ x ϵ R+
∴ x > 0)
∴ f एकैक है।
माना y = f(x) = x² + 4
= x² + 4 = y
x² = y – 4 = x = ±
लेकिन x धनात्मक है।
∴ x =
∴ f आच्छादक है।
अतः फलन f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f-¹(y) = g(y)
=
∀ y ≥ 4, 8 (y) एक धनात्मक मान है।
अतः फलन f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f-¹(y) = g(y)
=
∀ y ≥ 4, 8 (y) एक धनात्मक मान है।
अतः f का प्रतिलोम फलन =
प्रश्न 9.
f(x) = 9x² + 6x – 5 द्वारा प्रदत्त फलन f: R → [ – 5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f-1 = ((y+6√−1)3) है।
हल:दिया है : f(x) = 9x² + 6x – 5 तथा f: R → [ – 5, ∞)
माना y = 9x² + 6x – 5
= (3x + 1)² – 6
प्रश्न 10.
मान लीजिए कि f: x → y व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है।
हल:∵ यदि f एक व्युत्क्रमणीय है।
∴ gof (x) = Ix और fog (y) = Iy
⇒ f एकैक तथा आच्छादक है।
माना g1 व g2, f के दो प्रतिलोम फलन हैं।
∴ fog1 (y) = Iy तथा g0g2(y) = Iy
Iy दिए गये फलन f के लिए अद्वितीय है
∴ g1(9) = g2 (y) ⇒ f एकैक और आच्छादक है
अतः f का प्रतिलोम फलन अद्वितीय है।
प्रश्न 11.
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c द्वारा प्रदत्त फलन पर विचार कीजए। f-1 ज्ञात कीजिए और सिद्ध कीजिए कि (f-1)-1 = f है।
हल:दिया है :
f: {1, 2, 3} → a, b, d
तथा f(1) = a, f(2) = b, f (3) = c
माना x = {1, 2, 3} तथा y = {a, b, c}
इसलिए f: X → Y
∴ f-1 : Y → X
= f-1(a) = 1, f-1(b) = 2, f-1(c) = 3
इस फलन का प्रतिलोम फलन हम इस प्रकार से भी लिख सकते हैं
(f-1)-1 : x → y
⇒ (f-1)-1(1) = a, (f-1)-1
(2) = b, (f-1)-1(3) = c
इसलिए,
f: x → y
f(1) = a, f(2) = b, f(3) = c
अतः (f-1)-1 = f
प्रश्न 12.
मान लीजिए कि f:x → Y एक व्युत्क्रमणीय फलन है सिद्ध कीजिए कि f-1 का प्रतिलोम f, है अर्थात् (f-1)-1 = f है।
हल:f:x → Y एक व्युत्क्रमणीय फलन है।
∴ f एकैक तथा आच्छादक है।
⇒ g: y → x, जहाँ भी एकैक और आच्छादक है
∴ gof (x) = Ix तथा fog (y) = Iy
⇒ g = f
अतः f-1 o(f-1)-1 = I
fo[f-1 o(f-1)-1] = foI
⇒ (f of-1) o(f-1)-1 = f
Io(f-1)-1 = f
⇒ (f-1)-1 = f
प्रश्न 13.
यदि f :R → R, f(x) = (3 – x3)1/3, द्वारा प्रदत्त है तो fof(x) बराबर है.
(A) x1/3(B) x3
(C) x
(D) (3 – x3)
हल:
दिया है : f(x) = (3 – x3)1/3 तथा f: R → R
∴ fof(x) = f[f(x)] = [[(3 – x2)1/3]
= [3 – {(3 – x3 )1/3}3}]1/3
= [3 – (3 – x3)]1/3 = x
अतः विकल्प (C) सही है।
प्रश्न 14.
मान लीजिए कि f(x) = 4x3x+4 द्वारा परिभाषित एक फलन f: R – 1 – {−43} → R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R – {−43} , निम्नलिखित में से किसके द्वारा प्राप्त होगा-

हल:
दिया है : f(x) =
माना y =
∴ y(3x + 4) = 4x या 3xy + 4y = 4x
⇒ x(3y – 4) + 4y = 0
⇒ x =
अतः विकल्प (B) सही है।
NCERT Solution Variousinfo
तो दोस्तों, कैसी लगी आपको हमारी यह पोस्ट ! इसे अपने दोस्तों के साथ शेयर करना न भूलें, Sharing Button पोस्ट के निचे है। इसके अलावे अगर बिच में कोई समस्या आती है तो Comment Box में पूछने में जरा सा भी संकोच न करें। अगर आप चाहें तो अपना सवाल हमारे ईमेल Personal Contact Form को भर पर भी भेज सकते हैं। हमें आपकी सहायता करके ख़ुशी होगी । इससे सम्बंधित और ढेर सारे पोस्ट हम आगे लिखते रहेगें । इसलिए हमारे ब्लॉग “NCERT Solution Variousinfo” को अपने मोबाइल या कंप्यूटर में Bookmark (Ctrl + D) करना न भूलें तथा सभी पोस्ट अपने Email में पाने के लिए हमें अभी Subscribe करें। अगर ये पोस्ट आपको अच्छी लगी तो इसे अपने दोस्तों के साथ शेयर करना न भूलें। आप इसे whatsapp , Facebook या Twitter जैसे सोशल नेट्वर्किंग साइट्स पर शेयर करके इसे और लोगों तक पहुचाने में हमारी मदद करें। धन्यवाद !

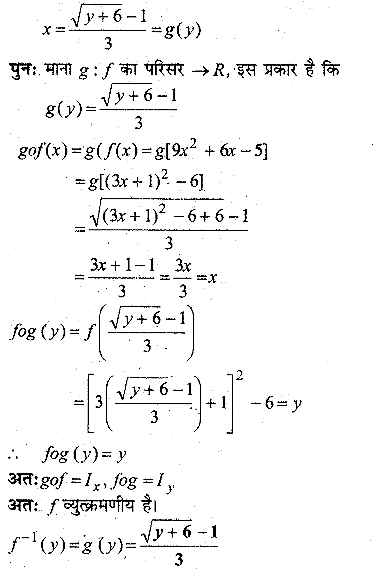
0 Response to "Class 12th maths notes chapter 1 Relationship and function ex1.3"
Post a Comment